Post

Survival Analysis

Posted Updated
By Lei Fang
26 min read
Survival Analysis
这是一份关于[Survival Analysis for Churn and Lifetime ValueDatabricks](https://www.databricks.com/solutions/accelerators/survival-analysis-for-churn-and-lifetime-value)的利用spark的复现报告。

01 初始设置

你首先需要保证你的server中拥有标准发行版的spark和mysql，并运行下列代码

1
2
3
4
5
6
7
8
9

# ! pip install lifelines

# ! pip install Matplotlib

# ! pip install numpy

# ! pip install pandas

# ! pip install seaborn

保证你的运行过程中支持相关的库函数。

本次报告针对的分析数据是raw.githubusercontent.com/IBM/telco-customer-churn-on-icp4d/master/data/Telco-Customer-Churn.csv，请确保下载后并配置好相应的文件存储位置。原教程由于是在databricks的环境中配置，许多代码及存储路径需要修改。可以模仿我的设置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Set config for database name, file paths, and table names

import getpass

  

user = getpass.getuser()  # Get the current username

username_sql = user.replace(".", "_")

database_name = f'dm_ibm_telco_churn_{username_sql}'

data_path = '/{}/ibm-telco-churn'.format(user)

driver_to_dbfs_path = '{}/Telco-Customer-Churn.csv'.format(data_path)

bronze_tbl_path = '{}/bronze/'.format(data_path)

silver_tbl_path = '{}/silver/'.format(data_path)

bronze_tbl_name = 'bronze_customers'

silver_tbl_name = 'silver_monthly_customers'

尤其需要注意的是，在运行00部分代码时，也行你的spark系统不包含hive及deltalake相关的jar包，笔者建议直接修改这些内容，将其设置为默认状况下的存储。因为本次分析并不会涉及到相关的事件使用。 如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# Construct silver table
  
  

# Load the CSV file into a DataFrame

bronze_df = spark.read.format('csv').schema(schema).option('header', 'true')\

               .load(driver_to_dbfs_path)
               
silver_df = bronze_df.withColumn('churn',when(col('churnString') == 'Yes',1).when(col('churnString') == 'No',0).otherwise('Unknown'))\

                     .drop('churnString').filter(col('contract') == 'Month-to-month')\

                     .filter(col('internetService') != 'No')
                 

而在sql的写入时，也应当修改为using parquet来避免类型的冲突。

1
2
3
4
5
6
7
8
9

_ = spark.sql('''

  CREATE TABLE `{}`.{}

  USING parquet

  LOCATION '{}'

  '''.format(database_name,bronze_tbl_name,bronze_tbl_path))

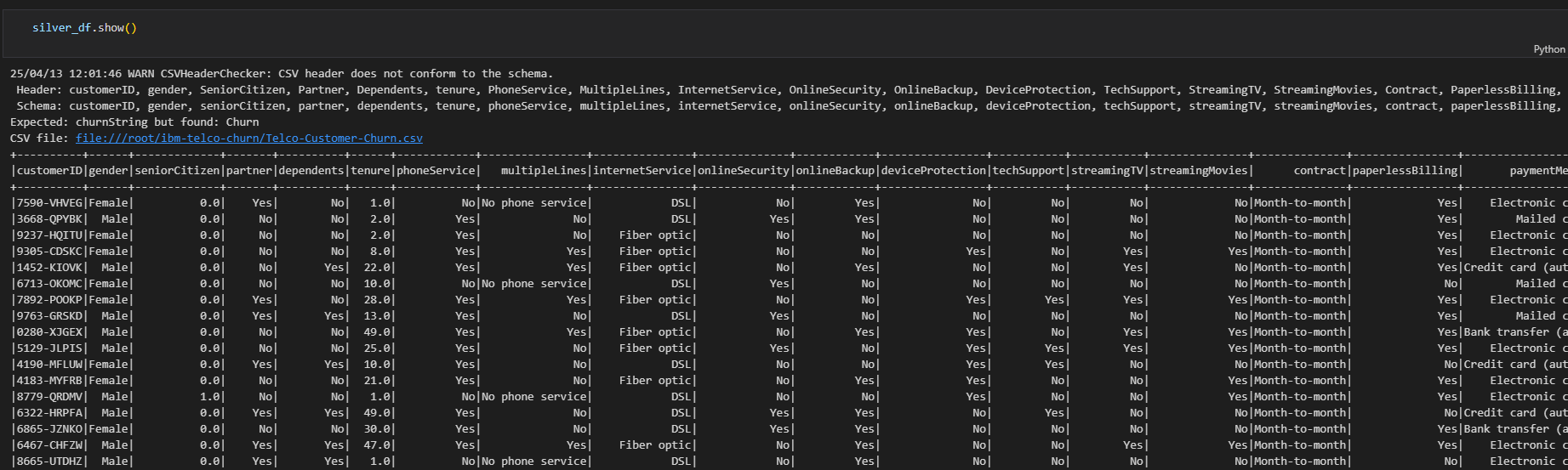
完成数据写入到数据库后，使用show()方法，你应当能检查到正常写入的数据库结果。 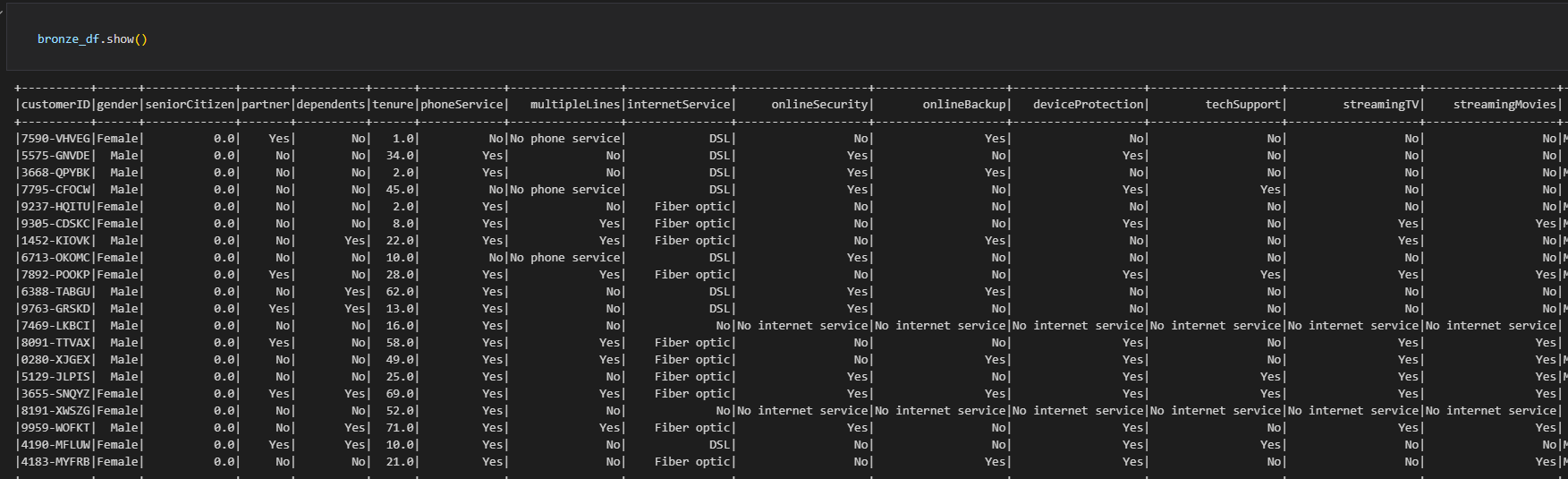ImageImage 下面开始正式的生存分析

生存分析是一组统计方法，用于检查和预测感兴趣事件发生之前的时间。这种形式的分析起源于医疗保健，重点关注死亡时间。从那时起，Survival Analysis 已成功应用于全球几乎每个行业的用例。 这次的分析是针对一个电信使用案例进行的，主要关注客户保留率，硬件故障和客户计划变化三个问题。 本次使用的数据集来自IBM，每条记录代表一个订阅者。其 在数据清洗的过程中，会得到一个新表silver，它是对于拥有month-to-month contract 的订阅者的另外记录。

02 Kaplan-Meier 生存概率曲线

在这一个小节，主要目的有：

  • 将 Kaplan-Meier 生存概率曲线拟合到 IBM 的 Telco 数据集。
  • 直观地评估总体水平和协变量水平的生存概率曲线。
  • 使用对数秩检验来确定生存曲线在统计上是否等效。
  • 提取生存概率以供后续建模。

拟合 Kaplan-Meier 模型

使用 Lifelines for Kaplan-Meier 的第一步是拟合模型。此步骤需要两个参数：tenure 和 churn。这里直接使用函数KaplanMeierFitter()即可

1
2
3
4
5
6
7

kmf = KaplanMeierFitter()

T=telco_pd['tenure']

C=telco_pd['churn'].astype(float)

kmf.fit(T,C)

目视评估群体水平的生存曲线

如下图所示，生存概率曲线在 x 轴上绘制了时间，在 y 轴上绘制了生存概率。 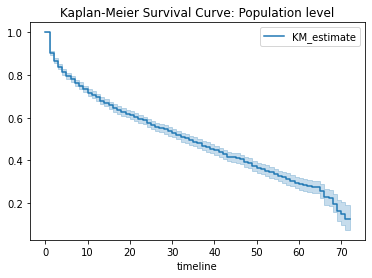Image生存概率曲线周围的浅蓝色边框表示置信区间。区间越宽，置信度越低。如下图所示，估计值的置信度随着时间线的增加而降低。虽然这种置信度降低可能是由于数据较少，但同样直观的是，我们对近期预测的信心比对长期预测的信心更大。

在协变量水平评估生存概率

  • 在协变量级别查看 Kaplan-Meier 曲线时，最好看到各组之间存在一定程度的差异，因为这表明可用于预测的差异。
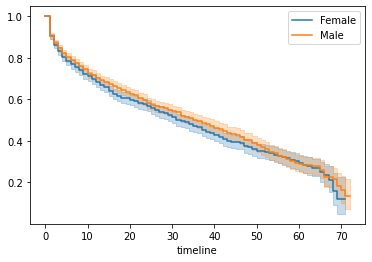
  • 有时生存曲线在预测时会非常接近，例如gender。这就是 log-rank 检验的目的。对数秩的原假设表明这些组在统计上是等效的。当p值大于0.05时，我们不能拒绝两组在统计上相等的假设。 Image
  • 在统计上相等并不代表没有意义。文中举了促销活动的例子，可以证明这样的发现有助于我们思考促销方针。

下图是onlineSecurity的曲线，一个明显有区别的例子 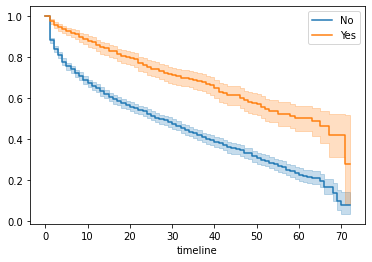Image之后文章对于每个变量都绘制了KM曲线并进行对数秩检验。节约空间，就不缀写了。 值得一提的是，只有phoneService 和gender的p值大于0.05，故认为这两组变量的影响在统计学上相等的可能性比较明显。其他变量都有把握认为对预测是有意义的。

提取结果

最后一步是将cox模型的结果提取出来，并将其用作a Customer Lifetime Value dashboard的输入。

03 Cox Proportional Hazards

这一节是对Cox Proportional Hazard 模型的拟合和讲解。

与 Kaplan-Meier 相比，Cox Proportional Hazards可用于多变量分析，且一样可用于绘制生存概率曲线。

模型解释

  • Cox Proportional Hazards用于估计风险比。风险比表示两个个体（或群体）之间存在的风险差异。危险本质上是生存的倒数，或者说失败的概率。
  • Cox 比例风险方程指出风险比是两个项的乘积：基线风险和部分风险。
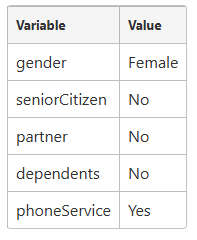
  • baseline hazard 只是一个 baseline，这是当每个变量都设置为特定值时存在的危险。在这里举了以下几个例子。Image
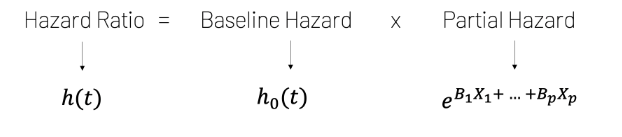
  • 偏风险表示当变量的值与基线不同时发生的风险变化。在任何给定时间，零个或多个变量可以包含与基线不同的值。如下面的方程式所示，由此产生的危险性变化是变量的线性组合。 Image
  • 如果每个变量都设置为其相应的基线值，则部分风险将等于 1（因为 e^0 = 1），风险比将等于基线风险。

The Proportional Hazards Assumption

Cox Proportional Hazard equation的一个微妙但关键的元素是基线风险是时间 t的函数，而不是参数的函数，而部分风险是参数的函数，而不是时间的函数。这支持了所谓的比例风险假设。比例风险假设指出，在 Cox 比例风险模型的上下文中，两组之间的风险比随时间成比例。这个假设隐含在上面的方程中，因为部分风险中没有 t 意味着部分风险比会改变某个因素，而与时间无关。 下面给出了成比例和不成比例的例子。 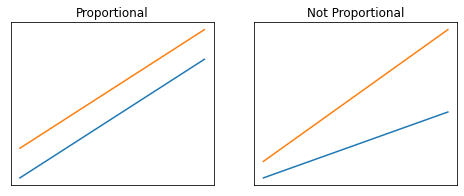Image

One-Hot 编码

对于分类变量，需要进行one-hot编码，以便使用lifelines库进行你和。这里手动选择了5个变量进行，并创建了一个新的dataframe进行分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# Encode columns of interest

encode_cols = ['dependents','internetService','onlineBackup','techSupport','paperlessBilling']

encoded_pd = pd.get_dummies(telco_pd,

               columns=encode_cols,

               prefix=encode_cols,

               drop_first=False)

encoded_pd.head()
# Create new dataframe consisting of only the variables needed to fit the model
# Cast churn column as a float

survival_pd.loc[:,'churn'] = survival_pd.loc[:,'churn'].astype('float')
survival_pd = encoded_pd[['churn','tenure','dependents_Yes','internetService_DSL','onlineBackup_Yes','techSupport_Yes']]

拟合模型

这里采用95%的置信区间进行统计测试。

评估拟合结果

考虑三个关键问题：

  • 每个协变量是否具有统计显著性？ 使用0.005作为p值分界，每列都具有显著性
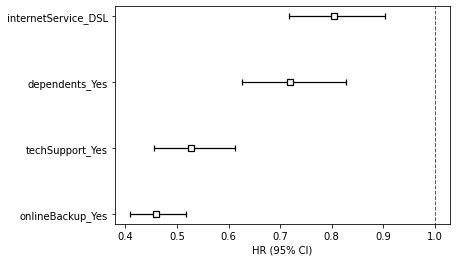
  • 我们对系数估计的置信度如何？ 取了exp的95%上下限，利用box-and-whisker plot可以直观观察。Image
  • 每个协变量对风险比有什么影响？ 以 internetService_DSL 为例，如下所示 coef = -0.22 和 exp（coef） = 0.80。回到 Cox 比例风险方程，这意味着当客户为其互联网服务订阅 DSL 时，其风险率降低了 0.80 倍（与基线相比）。

验证模型是否遵循比例风险假设

评估拟合模型的结果后，下一步是验证模型是否符合比例风险假设。我们将使用三种方法来做到这一点：

  • Method 1: Statistical Test
    方法 1：统计测试
  • Method 2: Schoenfield Residuals
    方法 2：Schoenfield 残差
  • Method 3: Log-log Kaplan-Meier Plots
    方法 3：log-log Kaplan-Meier 图

    统计测试

    从打印输出中可以看出，Lifelines 提供了相当多的细节，包括测试结果和建议。在这个模型的情况下，可以看出我们违反了四个变量中三个变量的比例风险假设。这可以通过小于 0.05 的 p 值及其下面的文本来说明。值得注意的是，正如 Kaplan-Meier 的结束语部分所暗示的那样，这种情况的一个危险信号是，当你在使用 Kaplan-Meier 时看到给定协变量的生存曲线相互交叉。

    1

    1. Variable 'internetService_DSL' failed the non-proportional test: p-value is <5e-05. Advice: with so few unique values (only 2), you can include `strata=['internetService_DSL', ...]` in the call in `.fit`. See documentation in link [E] below. Bootstrapping lowess lines. May take a moment... 2. Variable 'onlineBackup_Yes' failed the non-proportional test: p-value is <5e-05. Advice: with so few unique values (only 2), you can include `strata=['onlineBackup_Yes', ...]` in the call in `.fit`. See documentation in link [E] below. Bootstrapping lowess lines. May take a moment... 3. Variable 'techSupport_Yes' failed the non-proportional test: p-value is 0.0002. Advice: with so few unique values (only 2), you can include `strata=['techSupport_Yes', ...]` in the call in `.fit`. See documentation in link [E] below. --- [A] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html [B] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Bin-variable-and-stratify-on-it [C] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Introduce-time-varying-covariates [D] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Modify-the-functional-form [E] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Stratification Out[13]: [[<AxesSubplot:xlabel='rank-transformed time\n(p=0.3680)'>, <AxesSubplot:xlabel='km-transformed time\n(p=0.2232)'>], [<AxesSubplot:xlabel='rank-transformed time\n(p=0.0000)'>, <AxesSubplot:xlabel='km-transformed time\n(p=0.0000)'>], [<AxesSubplot:xlabel='rank-transformed time\n(p=0.0000)'>, <AxesSubplot:xlabel='km-transformed time\n(p=0.0000)'>], [<AxesSubplot:xlabel='rank-transformed time\n(p=0.0002)'>, <AxesSubplot:xlabel='km-transformed time\n(p=0.0044)'>]]

    Schoenfield 残差

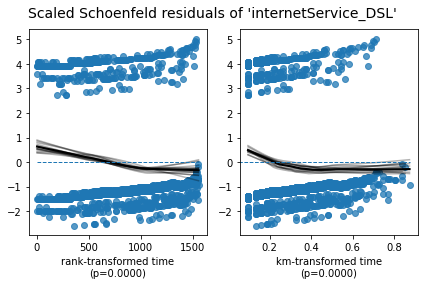
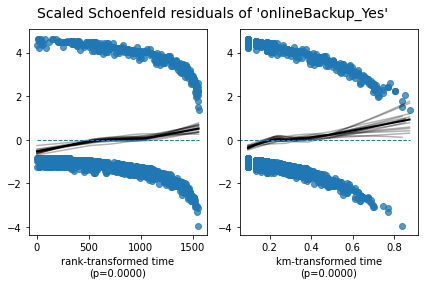
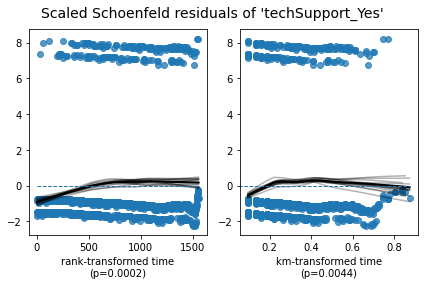
    除了运行统计测试之外，利用图形输出来评估情况也很有帮助。这可以使用 Schoenfeld 残差来完成。在下面的输出中，每个变量有两个图。这两个图之间的区别在于残差值的显示顺序： Rank transformed time 和 KM-transformed time。对于我们的模型，这两种类型的图之间没有观察到实质性差异。解释这些图的方法类似于解释线性回归的残差图的方法。换句话说，在查看这种类型的图时，我们不希望在残差中看到任何类型的模式。当不存在模式时，中间的黑线会比较平坦，表示残差与时间无关。 ImageImageImage Image

    ## Log-log Kaplan-Meier Plots

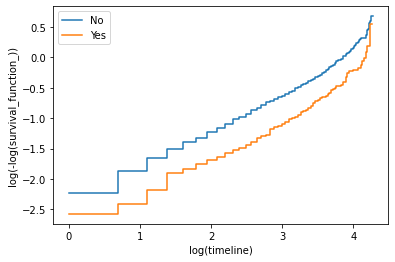
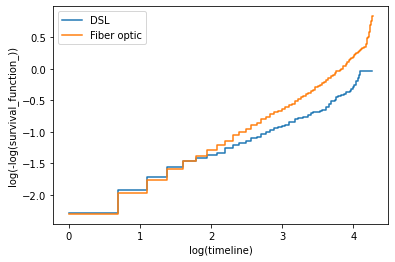
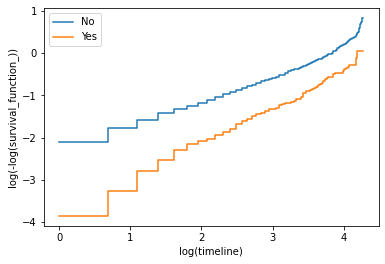
    根据统计检验的结果和 Schoenfeld 残差图，很明显，我们的模型多次违反了比例风险假设。为了从另一个角度了解这里的问题是什么，我们可以使用 log-log Kaplan-Meier 图。顾名思义，该技术在对数尺度上绘制 Kaplan-Meier 曲线。如果未违反比例风险假设，则对数图中的 Kaplan-Meier 曲线将显示为平行.

除了 internetService 之外，在下图中可以看到，当 log（timeline） 在 1 和 3 之间时，Kaplan-Meier 曲线大部分是平行的，但当 log（timeline） 小于 1 或大于 3 时，Kaplan-Meier 曲线是平行的。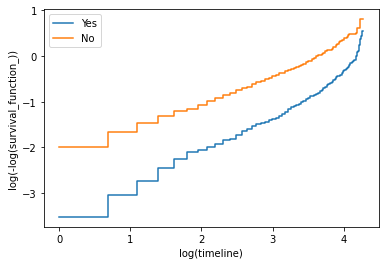ImageImageImageImage

04 Accelerated Failure Time

在这个部分，主要是对 Log-Logistic Accelerated Failure Time 模型进行学习。

Overview

这里举了狗的寿命作为例子，我们认为狗的衰老速度是人类的7倍，但他同样经历了和人相同的阶段，只是速度更快。这就是Accelerated Failure Time模型的灵感来源。它是一个参数化模型。这意味着假定结果变量服从指定的分布。参数化模型通常不如非参数和半参数模型“灵活”，但当面对分析指定结果变量的分布时，参数化模型可能是一个不错的选择。

基本假设

下面为AFT模型的方程，其中AB两组为不同的对象。而lambda尤其值得注意，它在实践当中往往是多个参数。例如log-logistic accelerated failure time is: $1/(1+\lambda \times t^ p)$. Image

one-hot 编码和环境配置

这里和03部分相似，不赘述

拟合模型

这里是使用log-logistic分布，故需要使用LogLogisticAFTFitter方法。

评估结果

同样是三个关键问题

  • 每个协变量是否具有统计显著性？ ** 可以看到每列的 p 值低于 < 0.005。因此，每列都具有统计显著性，可以安全地包含。
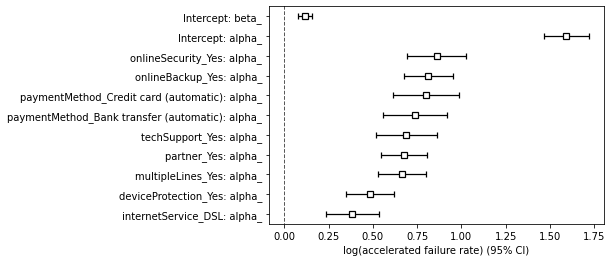
  • 我们对系数估计的置信度如何？ Image
  • 每个协变量对风险比有什么影响？ 以 internetService_DSL 为例，如 coef = 0.38 和 exp（coef） = 1.47。回到加速故障时间方程式，这意味着当客户将光纤作为其互联网服务时，客户的 it-until-churn 时间会加速 1.47 倍。请注意，Fiber Optic 是基线值，对应于上面共享的方程式中的 A 组。

验证假设

这里给出了不同变量的结果，下图为partner的，作为例子。分析结果如下。 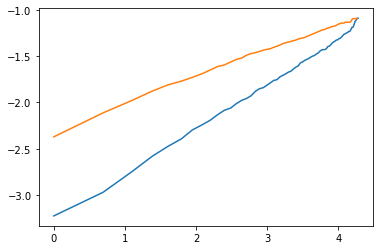Image 使用加速失效时间模型时，有两个基本假设需要评估：

  • 该模型是否遵循比例赔率假设？ 当图中的行平行时，答案是肯定的。
  • 指定的分布是否适合此模型？ 当线条是直的时，答案是肯定的。

我们的模型表现如何？

  • 在大多数情况下，每个图中的线条都相对笔直。有一些偏差，但总体上还不错。这意味着选择 log-logistic 作为指定的分布是一个合理的选择。
  • 在大多数情况下，每个图中的线条并不平行。这意味着 Accelerated Failure Time 不适用于指定的模型。

05 Customer Lifetime Value

在这个部分，完成了一个实际的工作流程，通过加载 IBM 的 Telco 客户流失数据集，并对部分变量进行独热编码，构建了一个用于生存分析的数据框。接下来，利用处理后的数据拟合了 Cox 比例风险模型，以评估客户的流失风险和寿命。

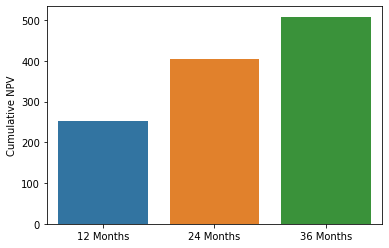
随后，通过创建交互式小组件（widgets），允许用户输入各项参数。基于这些参数，计算了客户在不同合约月份下的生存概率、预期月利润以及经过内部收益率折现后的净现值（NPV），并生成了一个包含累计 NPV 的数据表。最终，利用 seaborn 绘制了累计 NPV 和生存概率曲线图，这些图像有助于展示客户生命周期价值以及投资回收期。

数据加载与预处理

具体步骤如下：

  1. 数据加载
    从 Databricks 的银表 silver_monthly_customers 中加载数据，并转换为 Pandas DataFrame，确保在 Python 环境下可以对数据进行进一步处理。

  2. 数据编码
    针对多个分类变量（如 dependents、internetService、onlineBackup、techSupport、paperlessBilling 等），利用独热编码方法生成相应的虚拟变量。
    这一处理确保模型能够正确识别分类变量，并在后续建模过程中避免因类别歧义导致的不必要误差。

  3. 数据集构建
    在完成编码后，从整体数据集中提取出用于生存模型拟合的核心变量，包括：

    • 客户流失标识（churn），

    • 客户使用时长（tenure），

    • 编码后的特定变量（如 dependents_Yes、internetService_DSL、onlineBackup_Yes、techSupport_Yes）。

    特别注意对 churn 列的数据类型转换为 float，以便模型运算时保持数值一致性。

模型拟合及统计结果解读

基于预处理后的数据，使用 Lifelines 库拟合了 Cox 比例风险模型。该模型的拟合工作主要包括以下几个步骤：

  1. 模型定义与参数设定
    通过 CoxPHFitter 对象创建模型，并设置置信区间的显著性水平（例如 alpha=0.05）。

  2. 模型拟合
    利用 tenure 作为时间变量，churn 作为事件（右删失）变量，拟合模型，得到了包含 3351 个观测值、其中 1795 个为右删失的数据集。模型结果将用于评估各变量对客户流失风险的影响，并进一步判断模型是否满足比例风险假设。

  3. 统计输出解读
    通过对模型的统计输出和 Schoenfeld 残差图的分析，可以检测模型是否存在违反比例风险假设的情况，从而为后续调整或进一步细分分析提供依据。

仪表板开发与交互组件设计

为实现 CLV 的直观展示和业务决策辅助，本部分工作通过以下流程构建了一个包含数据表和可视化图表的仪表板：

  1. 小组件（Widgets）构建

    • 利用 Databricks 提供的 dbutils.widgets 模块，创建多个交互式小组件，允许用户选择或输入关键参数。例如选择 dependents_Yes、internetService_DSL、onlineBackup_Yes、techSupport_Yes 等变量的取值，另外还可以输入内部收益率（Internal Rate of Return）。

    • 用户通过这些小组件可以动态调整模型输入参数，从而实时观察参数变化对 CLV 分析结果的影响。

  2. 数据表构建

    • 通过函数 get_widget_values() 获取用户输入值，并构造数据框；

    • 使用模型的 predict_survival_function() 提取客户在各合约月份下的生存概率，

    • 基于生存概率、预设的固定月利润（此处示例值为 30），计算每月预期利润；

    • 结合内部收益率，通过净现值（NPV）公式折现预期利润，并计算累计 NPV，最终形成一个包含 Contract Month、Survival Probability、Monthly Profit、Avg Expected Monthly Profit、NPV of Avg Expected Monthly Profit 及 Cumulative NPV 的数据表。

  3. 图表绘制
    为便于直观了解客户利润的动态表现，笔记本通过 Seaborn 绘制了两类关键图表：

    • 累计 NPV 图表：展示不同合约期（例如 12、24、36 个月）下，累计净现值的分布情况，直观呈现客户获取成本和回收期；

    • 生存概率曲线图：绘制整个合约期内的客户生存概率曲线，辅助判断客户流失风险及 CLV 的变化趋势。 Image

Statistics, Survival Analysis, Big Data
Survival Analysis Statistics Data Science Spark
This post is licensed under CC BY 4.0 by the author.